weifoki.blogg.se - Linear model rstudio

lm can be used to fit a two-way ANOVA model: twoway.model |t|) Suppose our experiment involves two factors, treatment and time. # 1.1724940 0.4455249 1.9153967 4.2413688 9.1016661 -1.6877019įor a model with more than one coefficient, summary provides estimates and tests for each coefficient adjusted for all the other coefficients in the model. # F-statistic: 12.49 on 5 and 19 DF, p-value: 1.835e-05 coef(batch.model) # (Intercept) treatmentB treatmentC treatmentD treatmentE batchBatch2 # Residual standard error: 1.735 on 19 degrees of freedom We do this by adding the covariate “batch” to the model formula: batch.model |t|) Suppose we want to adjust for batch differences in our model.

The column treatmentC is 1 if an observation has treatment C and 0 otherwise.

The column treatmentB is 1 if an observation has treatment B and 0 otherwise.

The first column will always be 1 in every row if your model has an intercept.

(Note that “eatment”, or treatment contrasts, is how R refers to reference group coding) X # (Intercept) treatmentB treatmentC treatmentD treatmentE Sound complicated? The good news is that the design matrix can be specified through the model.matrix function using the same syntax as for lm, just without a response:ĭesign matrix for reference group coded model: X <- model.matrix(~treatment, data = dat) The design matrix \(\mathbf\) has one row for each observation and one column for each model coefficient.

Treatment B - treatment A, no-intercept model: coefs <- coef(no.intercept.model)Ĭoefs - coefs # treatmentBįor the RNASeq analysis programs limma and edgeR, the model is specified through the design matrix. Treatment B - treatment A, reference group coded model: coefs <- coef(oneway.model) The no-intercept model is the SAME model as the reference group coded model, in the sense that it gives the same estimate for any comparison between groups: Without the intercept, the coefficients here estimate the mean in each level of treatment: treatmentmeans # A B C D E # F-statistic: 31.66 on 5 and 20 DF, p-value: 7.605e-09 coef(no.intercept.model) # treatmentA treatmentB treatmentC treatmentD treatmentE

treatmentC is the mean of expression for treatment = C minus the mean for treatment = A.

treatmentB is the mean of expression for treatment = B minus the mean for treatment = A.

(Intercept) is the mean of expression for treatment = A.

Coefficients for other groups are the difference from the reference: The reference group doesn’t get its own coefficient, it is represented by the intercept. For categorical covariates, the first level alphabetically (or first factor level) is treated as the reference group.

The F-statistic compares the fit of the model as a whole to the null model (with no covariates)Ĭoef() gives you model coefficients: coef(oneway.model) # (Intercept) treatmentB treatmentC treatmentD treatmentE.

R-squared is (roughly) the proportion of variance in the outcome explained by the model.

Degrees of freedom is the sample size minus # of coefficients estimated.

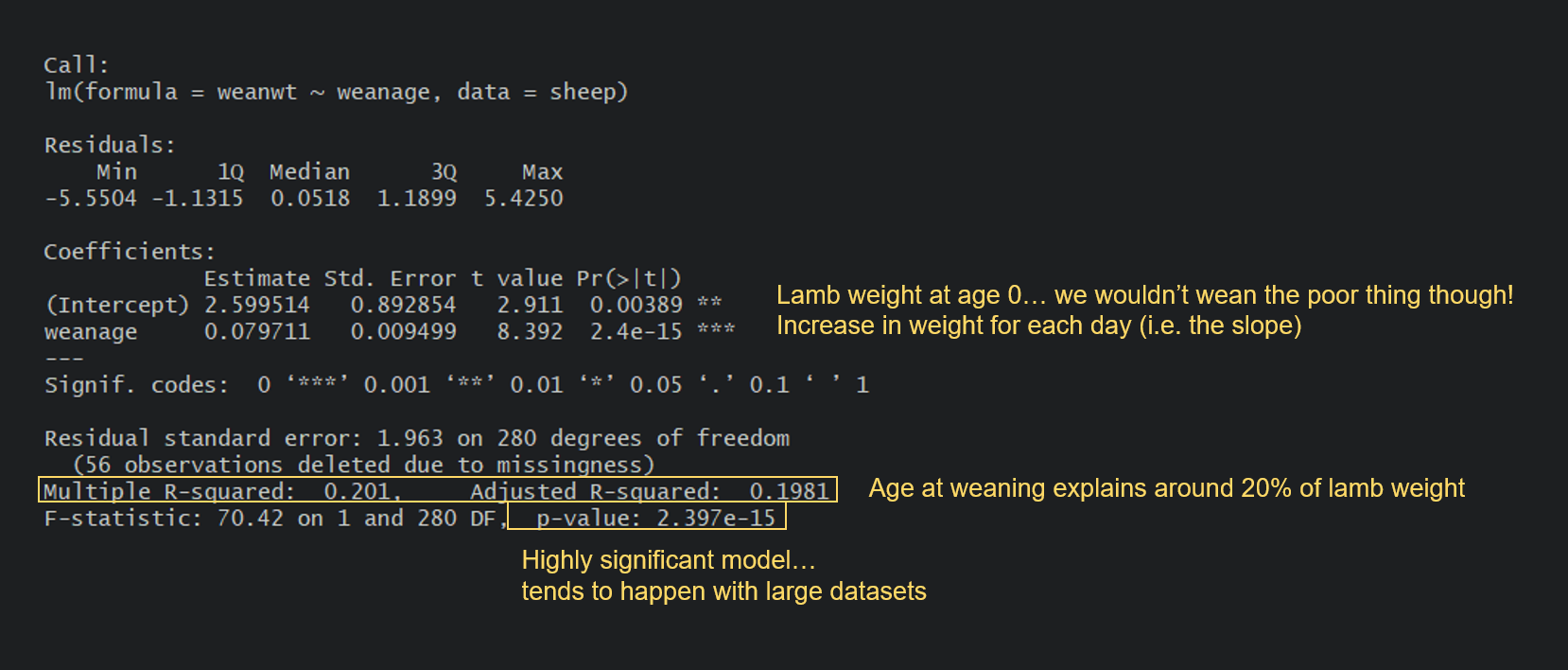
The residual standard error is the estimate of the variance of \(\epsilon\).“Pr(>|t|)” is the p-value for the coefficient.“t value” is the coefficient divided by its standard error.Error” is the standard error of the estimate

“Estimate” is the estimate of each coefficient.“Coefficients” refer to the \(\beta\)’s.

# Residual standard error: 1.74 on 20 degrees of freedom R uses the function lm to fit linear models.